Merkle Patricia Tree

2021-08-27 2 分钟阅读 区块链ManualBlockChain

区块链一个重要的亮点就是防篡改，那么它是怎么做到防篡改的呢？其中一个重要的知识点就是Merkle Patricia Tree(MPT)，本篇就来解析下何为MPT。

MPT是一种加密认证的数据结构，它融合了Merkle树和Patricia Trie树(基数树/压缩前缀树)两种数据类型的优点。

则在介绍MPT树之前先介绍下Merkle树(默克尔树)、Trie树(前缀树)和Patricia Trie(基数树/压缩前缀树)，介绍Trie树是因为Patricia Trie是基于Trie树衍化来的。

Trie树

Trie树又称前缀树或字典树，是一种检索树，使用一个有序的树结构存储一个动态数据集或者关联数组，其中的键通常是字符串。与二叉查找树不同，键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙相对于当前节点都有相同的前缀，而根节点为空字符串。一般情况下，不是所有的节点都有对应的值，只有叶子节点和部分内部节点所对应的键才有相关的值。

Trie树中，key是从树根到对应value得真实的路径。即从根节点开始，key中的每个字符会标识走那个子节点从而到达相应value。Value被存储在叶子节点，是每条路径的终止。假如key来自一个包含N个字符的字母表，那么树中的每个节点都可能会有多达N个孩子，树的最大深度是key的最大长度。看个例子画个图就了然了。 例子：关键字集合{“a”, “to”, “tea”, “ted”, “i”, “in”, “inn”}，此集合转为Trie树为

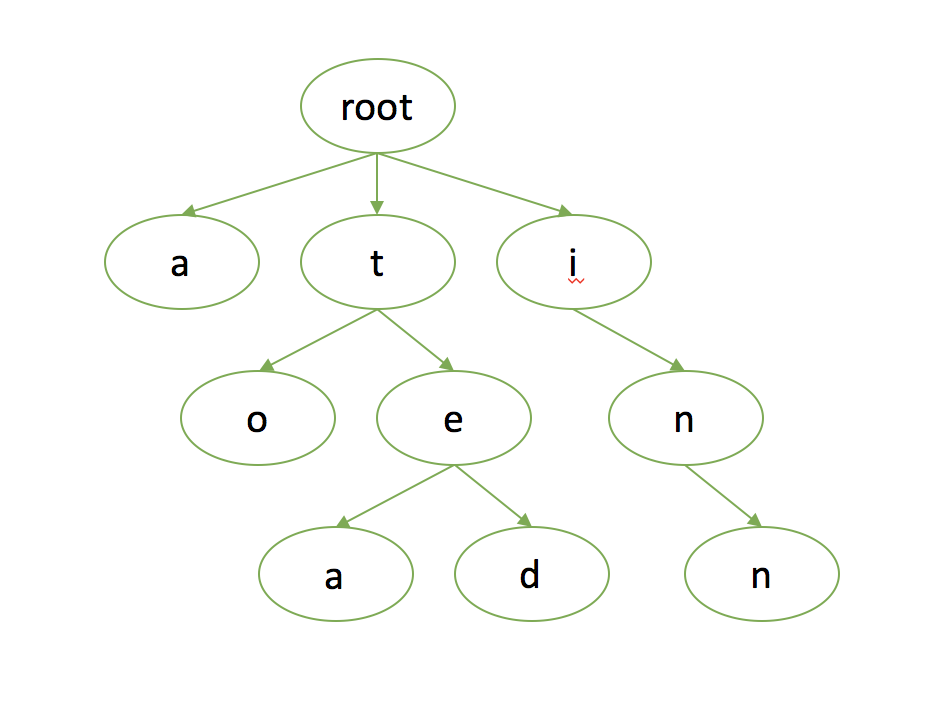img Trie树

不理想情况下，数据集中存在一个很长的key，而这个key与其它key又没有太多的公共前缀，这就造成整个树的深度会加大，需要存储多个节点，存储比较稀疏而且极不平衡。 例子：关键字集合{“algori”, “to”, “tea”, “ted”, “i”, “in”, “inn”}，此集合转为Trie树为

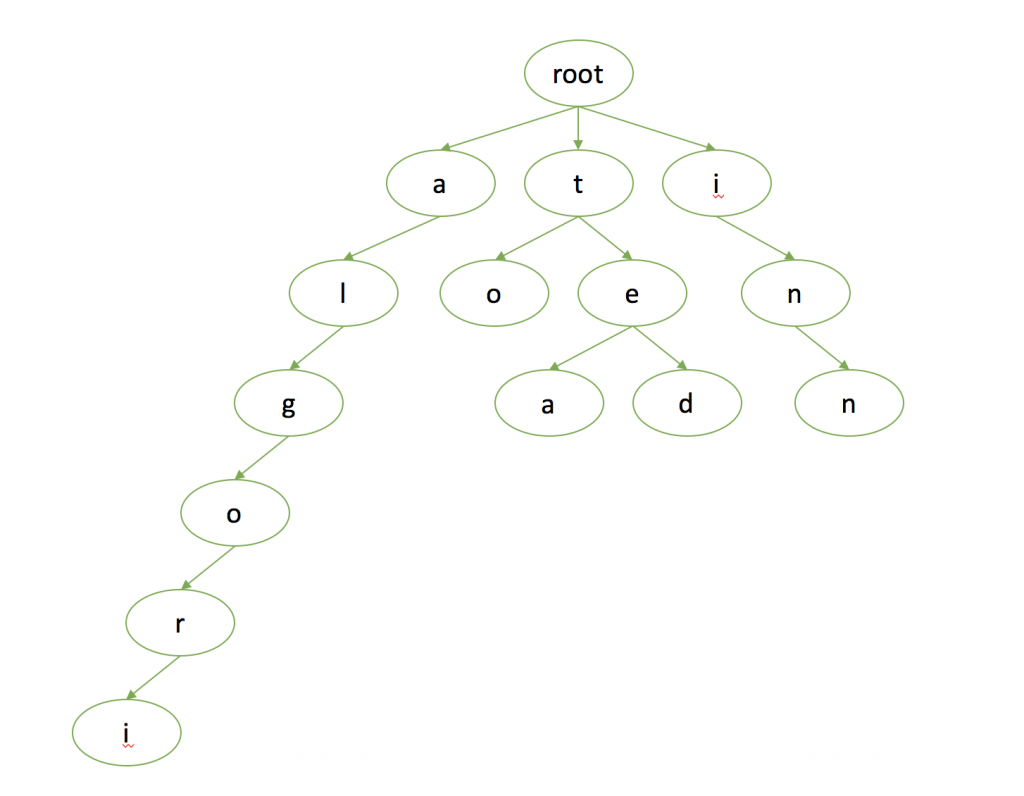img 稀疏Trie树

Patricia Trie树

既然Trie树在某些情况下存储空间利用率不高，那就给压缩下，然后就出现了Patricia Trie树。

Patricia Trie树是一种空间使用率经过优化的Trie树。与Trie树不同的是，Patricia Trie 里如果存在一个父节点只有一个子节点，那么这个父节点将与其子节点合并。这样压缩存储可以减少Trie树中不必要的深度，大大加快搜索节点速度。 如下图所示

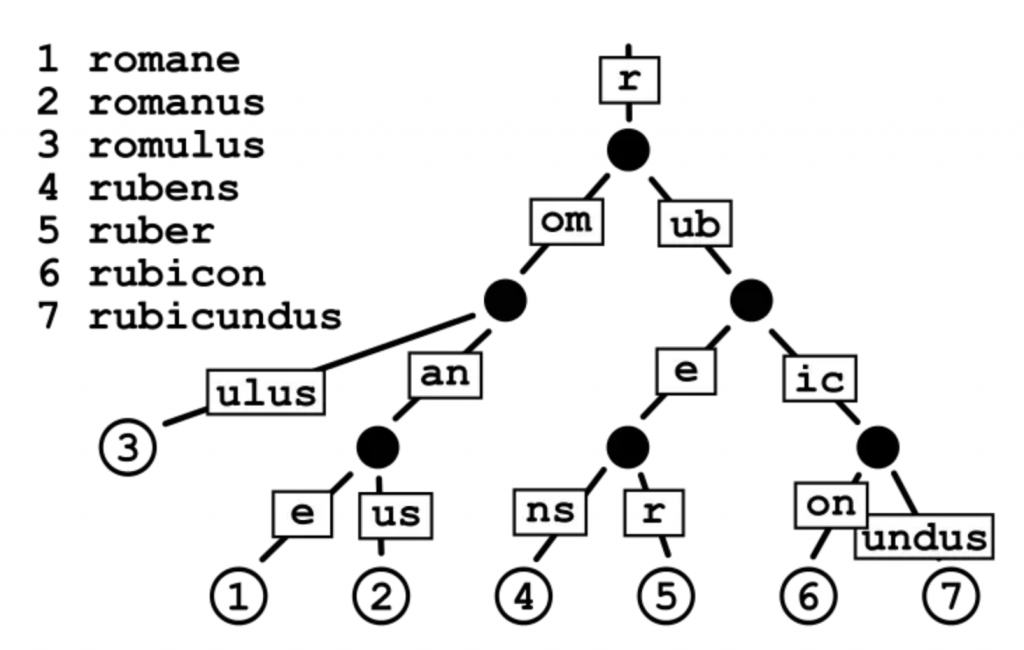img Patricia Trie树

Merkle树

Merkle树是由计算机科学家Ralph Merkle在很多年前提出的，并以他本人的名字来命名，是一种树形数据结构，可以是二叉树，也可以是多叉树。 它由若干叶节点、中间节点和一个根节点构成。最下面的叶节点包含基础数据，每个中间节点是它子节点的散列，根节点是它的子节点的散列，代表了Merkle树的根部。

由于Merkle树是自底向上构建的，而且除叶子结点之外的其它节点都是其子节点的散列，这样每个节点的值发生变化都会一层一层的向上反映，最终在根节点上表现出来。也就是说只要对比两个Merkle树的根节点是否相等就能得到两份数据集是否一样，而且还可以验证Merkle树的某个分支。

比特币使用Merkle树存储一个区块中的所有交易信息，一是为了防篡改，因为散列是向上的，伪造任何一个节点都会引起上层节点的改动，最终导致根节点的变化。二是为了允许区块的数据可以零散的传送，即节点可以从一个节点下载区块头，从另外的源下载与其相关的树的其他部分，而依然能够确认所有的数据都是正确的。

看下图的例子，首先将L1-L4四个单元数据散列化，然后将散列值存储至相应的叶子节点。这些节点是Hash0-0, Hash0-1, Hash1-0, Hash1-1，然后将相邻两个节点的散列值合并成一个字符串，然后计算这个字符串的散列，得到的就是这两个节点的父节点的散列值。

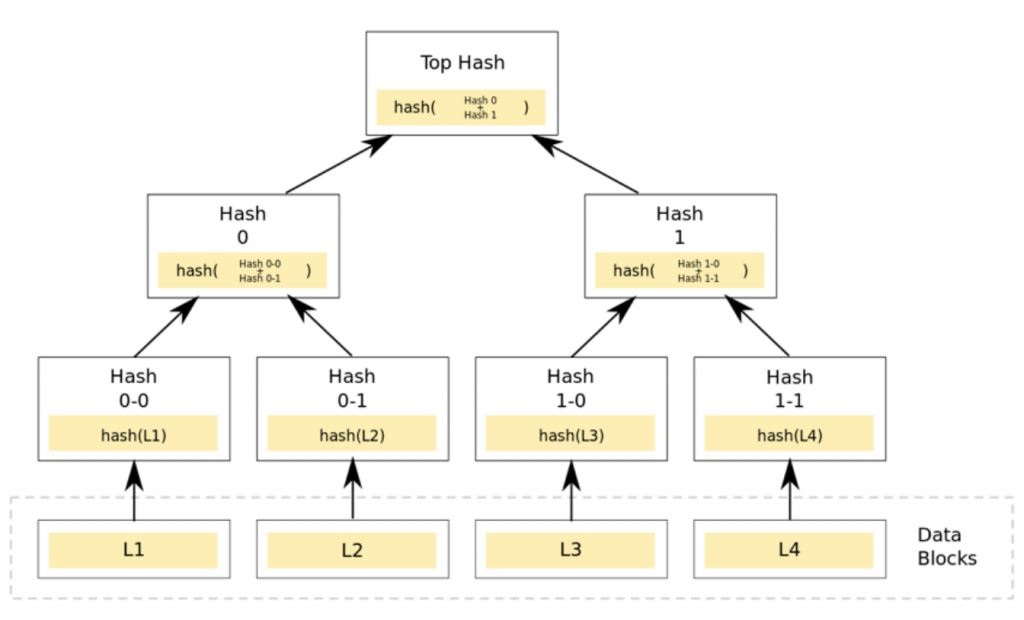img Merkle树

在比特币网络中，merkle树被用来归纳一个区块中的所有交易，同时生成整个交易集合的数字指纹。此外，由于merkle树的存在，使得在比特币这种公链的场景下，扩展一种“轻节点”实现简单支付验证变成可能。

知道了Merkle树在比特币中的应用，那么他是怎么构成呢？现在就简单看下其构成。它由一组叶节点、一组中间节点和一个根节点构成。最下面的叶节点包含基础数据，每个中间节点是它的子节点的散列，根节点是它的子节点的散列，代表了Merkle树的根部 。

Merkle树具有下列特性:

  1. 每个数据集对应一个唯一合法的根散列值。
  2. 很容易更新、添加或者删除树节点，以及生成新的根散列值 。
  3. 不改变根散列值的话就没有办法修改树的任何部分，所以如果根散列值被包括在签名的文档或有效区块中，就可以保证这棵树的正确性。
  4. 任何人可以只提供一个到特定节点的分支，并通过密码学方法证明拥有对应内容的节点确实在树里 。

Merkle Patricia Tree

叨叨了那么多，本篇的主角终于出来了。 Merkle Patricia Tree结合了Merkle树和Patricia树的特点，并针对以太坊的使用场景进行了一些改进。

首先，为了保证树的加密安全，每个节点通过它的散列值被引用，则根节点是一层一层散列向上收敛而得，被称为整棵树的加密签名，如果一棵给定 Trie树的根散列值是公开的，那么所有人都可以提供一种证明，即通过提供每步向上的路径证明特定的key是否含有特定的值。在当前的以太坊版本中，MPT存储在LevelDB数据库中。

其次，MPT树引人了很多节点类型来提高效率。包括以下4种:

  • 空节点(NULL) – represented as the empty string

简单的表示空，在代码中是一个空串。

  • 叶子节点(leaf) – a 2-item node [encodedPath, value]

表示为[key,value]的一个键值对，其中key是key的一种特殊十六进制编码(MP编码)， value是value的RLP编码。

  • 分支节点(branch) – a 17-item node [v0 … v15, vt]

因为MPT树中的key被编码成一种特殊的16进制的表示，再加上最后的value，所以分支节点是一个长度为17的list，前16个元素对应着key中的16个可能的十六进制字符，如果有一个[key,value]对在这个分支节点终止，最后一个元素代表这个值value，即分支节点既可以是搜索路径的终止也可以是路径的中间节点。

  • 扩展节点(extension) – a 2-item node [encodedPath, key]

也是[key，value]的一个键值对，但是这里的value是其他节点的hash值，这个hash可以被用来查询数据库中的节点。也就是说通过hash链接到其他节点。

下面看个以太坊中MPT树的官方示例

img

示例

看到这里你肯定依然是一脸懵逼，(不要问我我是怎么知道的。。。。)，接下来我们就来根据一批数据构造一个MPT树，这样你会理解一些。 但是在讲例子之前，还得先介绍几种编码方式，要不看例子的时候对key的取值会比较懵。

key编码

在以太坊中，MPT树的key值共有三种不同的编码方式，分别为:

  1. Raw编码(原生的字符)
  2. Hex编码(扩展的16进制编码)
  3. Hex-Prefix编码(16进制前缀编码)
Raw编码

Raw编码就是原生的key值，不做任何改变。这种编码方式的key，是MPT对外提供接口的默认编码方式。
例如key为”dog”，value为”puppy”的数据项，其key的Raw编码就是[‘d’, ‘o’, ‘g’]，换成ASCII表示方式就是[64, 6f, 67] : dog => ‘puppy’

Hex编码

Hex编码就是把一个8位的字节数据根据高4位和低4位拆解为两个4位的数字，然后两个数字的高4位都补0，最后将补完之后的两个字节编码为16进制。
这里需要注意的是key对应的值为真实的数据项，即是一个有意义的kv对，比如dog->puppy(也就是叶子结点)，而不是key->节点hash(也就是分支节点)，则在末尾添加一个ASCII值为16(十六进制为0x10)的字符串作为terminator。如果是分支节点则不加任何字符。
例如key为”dog”，value为”puppy”的数据项，其key中d(100)的二进制编码为01100100，拆解为两个4位的数字为0110和0100，高位补0之后的二进制为00000110和00000100，16进制为6和4，依次编码o和g。又因为dog对应的value是真实的数据项，则在末尾添加16。最后最终的Hex编码为[ 6, 4, 6, 15, 6, 7, 16 ] : dog => ‘puppy’

Hex-Prefix编码

首先根据名字得知这是一个前缀编码，是在原key的基础上加上一些标识作为前缀，其次我们看下这种编码方式的目的：
1. 区分leaf和extension
2. 把奇数路径变成偶数路径

则这个前缀的生成肯定与leaf、extension和key的奇偶相关了，下面看下编码步骤为:
1. 先按Hex对key进行编码
2. key的结尾如果是0x10(也就是16)，则去掉这个终止符
3. key之前补一个四元组，这个四元组第0位区分奇偶信息，第1位区分节点类型，表格表示如下
node type path length prefix hexchar
extension even 0000 0x0
extension odd 0001 0x1
leaf even 0010 0x2
leaf odd 0011 0x3 
4. 如果输入key的长度是偶数，则在之前的四元组后再添加一个四元组0x0
5. 将原来的key内容压缩，将分离的两个byte以高四位低四位进行合并

这里有个名词解释下，四元组是四个bit位的组合(例如二进制表达的0010就是一个四元组)，其中Nibble就是一个四元组，是key的基本单元。

例如key为”dog”，value为”puppy”的数据项，则首先对dog进行Hex编码[ 6, 4, 6, 15, 6, 7, 16 ]，然后按照上面的步骤进行编码，dog的Hex编码末尾是16，去掉终止符为[ 6, 4, 6, 15, 6, 7 ]，准备在key前补四元组，dog为叶子节点并且编码之后的长度为6是偶数，所以四元组为0010(0x2)，此时到了第4步，key编码之后的长度是偶数，则在前一个四元组(0x2)之后再添加一个四元组0x0，最终的前缀为0x20。最后将原来的key内容进行高低四位合并，最终的Hex-Prefix编码是[ 0x20, 0x64, 0x6f, 0x67 ]

以上三种编码方式的转换关系为：

Raw编码: 原生的key编码，是MPT对外提供接口中使用的编码方式，当数据项被插入到树中时，Raw编码被转换成Hex编码
Hex编码: 16进制扩展编码，用于对内存中树节点key进行编码，当树节点被持久化到数据库时，Hex编码被转换成HP编码
HP编码: 16进制前缀编码，用于对数据库中树节点key进行编码，当树节点被加载到内存时，HP编码被转换成Hex编码

构造过程

接下来我们就实际操作下： 假设我们有一个树有这样一些kv对(‘dog’, ‘puppy’), (‘horse’, ‘stallion’), (‘do’, ‘verb’), (‘doge’, ‘coin’)。 首先，我们将key转成Hex编码，如下：

# 64 6f
[ 6, 4, 6, 15, 16 ] : do => 'verb'
#64 6f 67
[ 6, 4, 6, 15, 6, 7, 16 ] : dog => 'puppy'
#64 6f 67 65
[ 6, 4, 6, 15, 6, 7, 6, 5, 16 ] : doge => 'coin'
#68 6f 72 73 65
[ 6, 8, 6, 15, 7, 2, 7, 3, 6, 5, 16 ] : horse => 'stallion'

其构造MPT树如图：

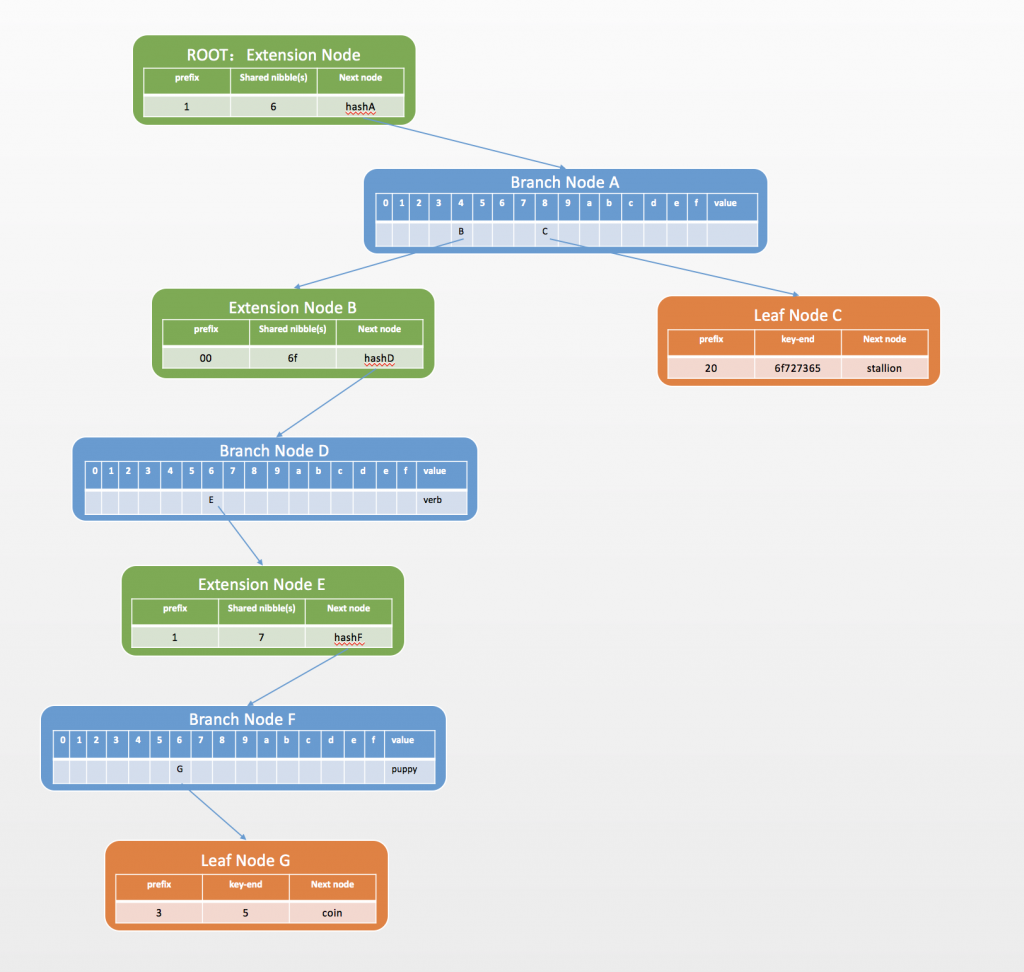img MPT

rootHash: [ <16>, hashA ]
hashA:    [ <>, <>, <>, <>, hashB, <>, <>, <>, hashC, <>, <>, <>, <>, <>, <>, <>, <> ]
hashC:    [ <20 6f 72 73 65>, 'stallion' ]
hashB:    [ <00 6f>, hashD ]
hashD:    [ <>, <>, <>, <>, <>, <>, hashE, <>, <>, <>, <>, <>, <>, <>, <>, <>, 'verb' ]
hashE:    [ <17>, hashF ]
hashF:    [ <>, <>, <>, <>, <>, <>, hashG, <>, <>, <>, <>, <>, <>, <>, <>, <>, 'puppy' ]
hashG:    [ <35>, 'coin' ]

构造过程为 假设插入第一个kv对是do->verb，key根据Hex-Prefix编码为[‘0x20’, ‘0x64’, ‘0x6f’]，MPT树为：

  1. 假设插入第一个kv对是do->verb，key根据Hex-Prefix编码为[‘0x20’, ‘0x64’, ‘0x6f’]，MPT树为：

img 叶子节点

  1. 接着插入第二个kv对dog->puppy，dog和do的公共前缀为[‘64’, ‘6f’]，do是叶子结点A，将叶子结点替换成扩展节点A，并将新key与叶子节点A的公共前缀(646f)作为扩展节点的key，扩展节点的value是新分支节点B的hash值，然后将do和dog剩余的key插入到分支节点中，由于do没有剩余的key，则将对应的value写入分支节点B的value中，dog剩余的key为67，则分支节点B中的路径为6，指向叶子结点C。7为dog剩下的最后一个key值，是奇数叶子结点则前缀为3，所有最终的MPT树为：

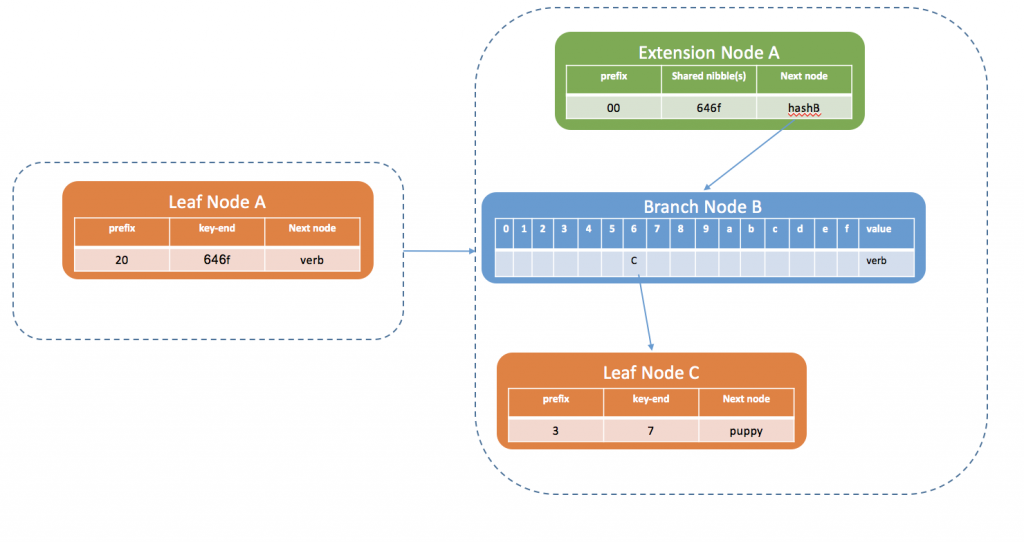img 叶子节点插入

  1. 再插入第三个kv对doge->coin，按照上面的步骤生成的MPT树是：

img

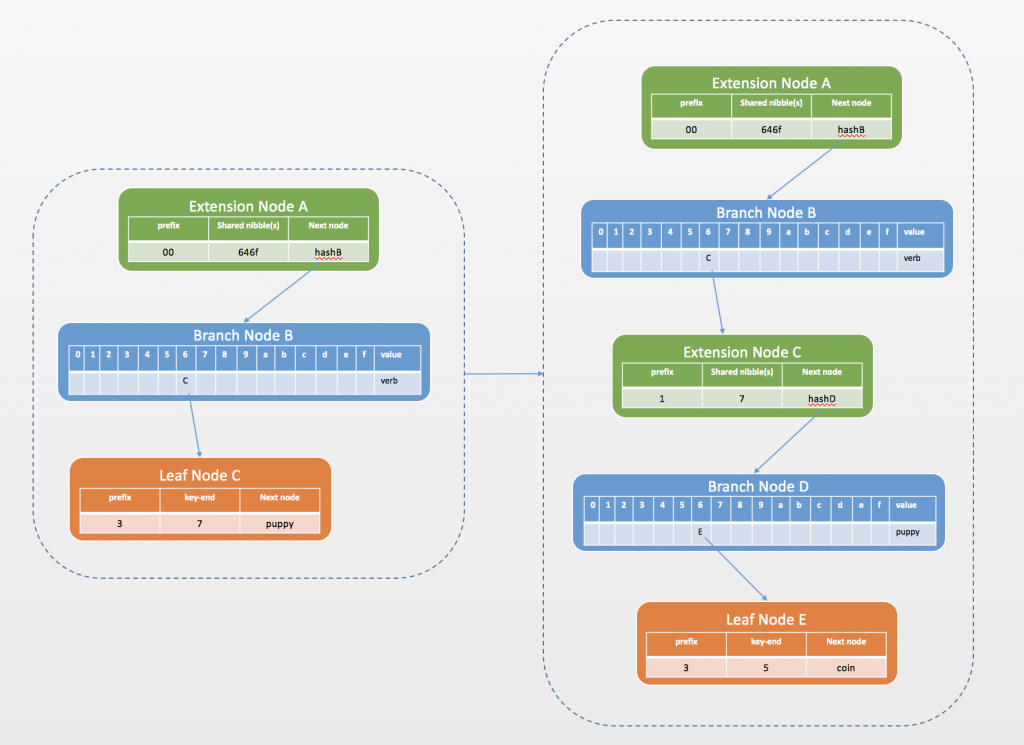
  1. 最后插入第四个kv对horse->stallion，horse与其它key的公共前缀只有6，则将扩展节点A新增一个分支节点F作为其孩子节点，将新key与扩展节点A的公共前缀6作为扩展节点A的key，A是扩展节点并且key为奇数，所以前缀为1，value为新增分支节点F的hash。原扩展节点A变成新扩展节点之后剩余的key，与新key剩下的key，插入到分支节点F中，分别放入4和8中，4指向新的扩展节点G，8指向叶子节点H。最终的MPT树为：

img

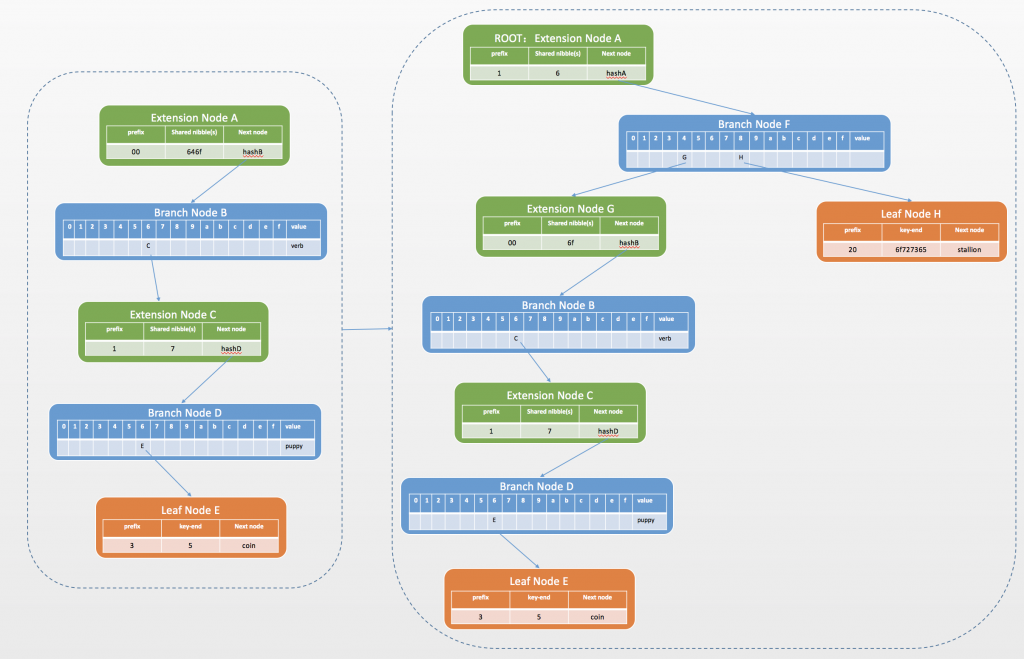
MPT在以太坊中的应用

Merkle数据结构在区块链领域中使用比较广泛，比特币和以太坊都是用了Merkle树，其中以太坊中保留了三颗MPT，分别是状态树、交易树和收据树，这三种树可以帮助以太坊客户端做一些简易的查询，如查询某个账户的余额、某笔交易是否被包含在区块中等。

需要注意的是在以太坊中对MPT再进行了一次封装，对数据项的key进行了一次哈希计算sha3(key)，value进行了RLP(Recursive length prefix encoding,递归长度前缀编码)编码，数据库中存储额外的sha3(key)与key之间的对应关系。

原文链接：

http://bigdatadecode.club/Merkle-Patricia-Tree.html

MongoDB综述
Maven基础

版权

相关文章

评论